Конспект уроку алгебри в 10 класі

Тема: Основні способи розв’язування тригонометричних рівнянь . Рівняння, що зводяться до квадратних.

Мета: Провести огляд основних способів розв’язування тригонометричних рівнянь. Домогтися засвоєння схеми дій під час розв’язування рівнянь, що зводяться до квадратних відносно тригонометричних функцій; формувати уміння розв’язувати тригонометричні рівняння такого типу.

Розвивати навички застосовувати потрібні тригонометричні формули  та властивості обернених тригонометричних  функцій до розв’язування рівнянь даного типу.

Сприяти вихованню рис  акуратності, цілеспрямованості, взаємодопомоги.

Тип уроку: засвоєння знань, формування умінь.

Наочність та обладнання: підручник Алгебра 10 клас (А.Г.Мерзляк), конспект уроку, комп’ютери, комп'ютерна презентація, програма для складання комп'ютерних тестів Test-W2.

Хід уроку

1. Організаційний момент.
2. Перевірка домашнього завдання. Комп’ютерне тестування учнів з теми «Обернені тригонометричні функції».
   
   
   Скриншоти тестів
   
3. Актуалізація опорних знань учнів:

Теоретичні відомості: презентація.

​

               Усні вправи на дошці:

• Обчислити: arcsin0, arcсos 1 , arctg (-1) , arcos (- 1/2  );
• Яке з рівнянь немає розв’язків: sin x=1; cosx=-1; sinx=4; cosx=-3; tgx=15; ctgx=0,5;
• Розв’язати квадратне рівняння: 2x²+x-1=0

4. Пояснення нового матеріалу.

Огляд основних способів розв’язування тригонометричних рівнянь

Найчастіше зустрічаються тригонометричні рівняння таких видів:

• Найпростіші тригонометричні рівняння, та рівняння, що зводяться до найпростіших:
• Тригонометричні рівняння, що зводяться до квадратних
• Тригонометричні рівняння, що розв’язуються методом розкладання на множники
• Однорідні тригонометричні рівняння​

Ознайомлення учнів з алгоритмом розв’язування рівнянь, що зводяться до квадратних відносно тригонометричних функцій

Сьогодні ми розглянемо такий спосіб розв’язування тригонометричних рівнянь, як зведення до квадратного. При розв’язуванні рівнянь такого типу можна користуватися таким алгоритмом:

1. Знайти ОДЗ рівняння. Якщо тригонометричне  рівняння цілого виду містить тільки синуси і косинуси то ОДЗ будуть всі дійсні числа. Тому під час розв’язання рівнянь типу: 6cos²x+5sinx-7=0 область визначення можна не визначати.
2. Якщо рівняння містять різні тригонометричні функції або різні аргументи, то звести рівняння до однієї тригонометричної функції та одного аргументу.
3. Ввести заміну.
4. Розв’язати отримане квадратне рівняння.
5. Повернутися до початкової заміни і ров’язати утворені найпростіші тригонометричні рівняння.
6. Записати відповідь з урахуванням ОДЗ рівняння.

Пояснення нового матеріалу (На конкретному прикладі)

5. Формування умінь учнів. Робота з підручником. Розв’язування номерів :№831 (2),№831(5),№835(1),№835(3)

№831

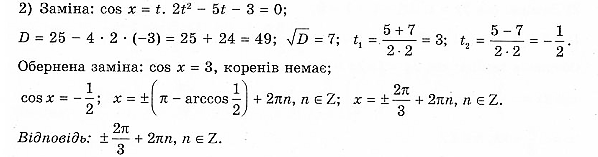
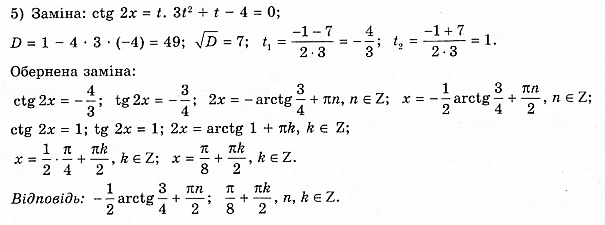
№835

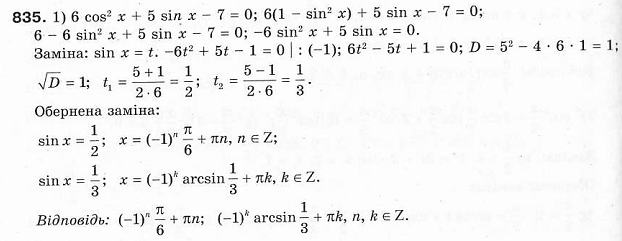
№835 (3)

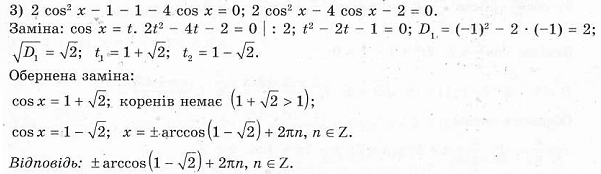
6. Підсумок уроку. Домашнє завдання: Опрацювати п. 35. (Приклад 1). №831.(3); №832.(1,2); №836(1)

7. ---

    Фото з уроку